Animal —Turtles

This is an “elemental research” category page. It outlines interests around a specific topic. The links at the bottom lead to mostly photographic documentation of experiments and projects that touch on the topic.

Turtles:

Taxonomy:

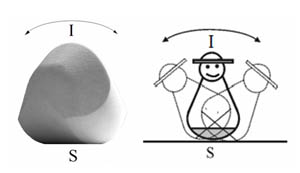
In 2006 Hungarian mathematicians Gábor Domokos and Péter L. Várkonyi demonstrated the possibility of “a convex three-dimensional homogeneous body which, when resting on a flat surface, has just one stable and one unstable point of equilibrium.” They named such forms Gömböc after a sweet Hungarian dumpling. Gömböc are self-righting: they will roll as if possessed before coming to rest on one precise point.

In 2007 the same mathematicians authored a paper examining the surprising similarity between Gömböc and certain turtle species. By providing turtles with shaped shells that allow them to avoid the certain death that finding themselves on their backs portends, evolution anticipated the discovery of the Gomboc by millennia.
Later that year the Gömböc-Shop.com was launched, offering authentic forms for purchase. Proof that Gomboc exist has been published, however the precise geometry necessary for their construction has not been made public.

Domokos and Varkonyi found a solution to an abstract mathematical puzzle and provided insight into a natural form.  Their findings also answered an age-old artistic question – how can one make three-dimensional multiples where each object can only be displayed in a single way?
see (Not)Turtles in Projects Section of this site

FROM: J. Nonlinear Sci. Vol. 16: pp. 255–281 (2006)
DOI: 10.1007/s00332-005-0691-8:

Summary. By appealing to the Poincaré–Hopf Theorem on topological invariants, we introduce a global classification scheme for homogeneous, convex bodies based on the number and type of their equilibria.We show that beyond trivially empty classes all other classes are non-empty in the case of three-dimensional bodies; in particular we prove the existence of a body with just one stable and one unstable equilibrium. In the case of two-dimensional bodies the situation is radically different: the class with one stable and one unstable equilibrium is empty (Domokos, Papadopoulos, Ruina, J. Elasticity 36 [1994], 59–66). We also show that the latter result is equivalent to the classical Four-Vertex Theorem in differential geometry.We illustrate the introduced equivalence classes by various types of dice and statistical experimental results concerning pebbles on the seacoast.

Research associated with Turtles: